こんにちは、ミスターステップアップの村田明彦です。
今回は、共通テスト数学の過去問の勉強法について、説明していきます。
ぜひここで紹介している勉強法を参考にして、共通テスト数学で高得点を目指してください。
【動画】<共通テスト数学>3ヶ月で9割とれる!受験生必見のすごい対策
1.共通テスト数学で高得点を取るための勉強法のコツ
共通テスト数学で高得点を取るための勉強法のコツについて、説明していきます。
1-1.共通テスト数学攻略におすすめの参考書
どのシリーズでもかまいませんので、7回以上反復練習して、スラスラと正解が書けることを目標にしましょう。
1-2.共通テスト数学の過去問の活用法
過去問を活用するにあたり、過去問の研究はとても重要です。
出題内容を見たときに、共通テストの場合は誘導に乗れるかがとても大切になってきます。
どういう風に考えればよかったのか、この場面では何の公式を使うべきだったのか、というように、復習・反省をしないと成績は伸びていきません。
最低でも過去問5年分はしっかり復習して、解き方も考え方も全部わかっている状態にすることが重要です。
実際にミスターステップアップの塾生からの質問を元に、具体的なやり方を説明したいと思います。
例えば、センター数学の2013年1Aの大問3を見てみましょう。
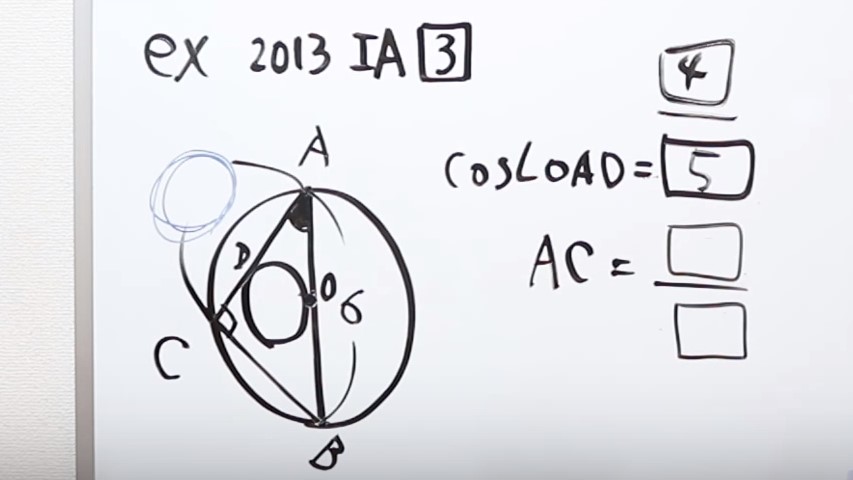
この問題のACの長さを求めるところで詰まってしまい、ひらめかなかったとします。
この問題では、与えられている条件で直角三角形のACの長さを求める。
ACを求める前に、斜辺がわかっており、コサインOADが与えられているので、三角比の計算からACは、斜辺分のACでコサインが求められる。
これは、直角三角形の三角比で一番最初に習う内容です。
コサインというのは、斜辺分の横の長さで計算できます。斜辺は6なので、
AC/6=4/5
AC=24/5
このようにACの長さが求められます。
蓋を開けたら、簡単にわかることだと思いますが、実際の問題の中に溶け込んでいたりすると、わからなかったり、ひらめかなかったりすることがあります。
このように、過去問で詰まったところや間違えたところは、放置せずに言語化するようにしましょう。
言語化するために、「FOR(Frame Of Reference 、知的判断枠組)」を作るようにします。
例えば、直角三角形を見たら、何を考えなければならないのか。
-
辺の長さを求める問題だったら、まずは三平方を考える
-
三平方でなかったら、三角比から判断する
-
サイン、コサイン、タンジェントが与えられていないかを確認する
-
相似の三角形があるか確認する
といったように、どういった可能性が考えられ、何の公式を使うことができるのかを、全部言葉にできる状態を作っておきます。
そして、そこから一個一個、選択肢をつぶしていくと、たいてい閃きます。
もし、閃かなかったところは、普段から言語化ができていないのです。
ですので、そこを意識して何回も反復することをおすすめします。

ミスターステップアップの卒塾生の永井くんは、「知的判断枠組」のノートを作るようになってから成績が伸び始め、見事国立医学部に合格しました。
彼のノートには、間違えたところが全部書いてありました。
- 「円の直径になっていることを確認しましたか?」
- 「サインを求める時は、正弦定理から求めますか?」
- 「正弦定理で他の角から求めますか?」
- 「面積は考えましたか?」
といったようにです。
永井くんのように自分の言葉でいいので、間違えるたびに抽出していきます。
そして全部言語化し、例えば「図形と計量の範囲はこの1枚の紙の中に全部収まっていて、ここに載っている考え方だけで絶対に解ける」という状態にします。
このように、ストックを作っていくようにするのです。
ストック量がたくさん増えていったら、間違えたところをとにかく意識して、カラダで覚えるくらいまで反復するようにしていきます。
最終的に永井くんは、センター数学で9割以上取ることができ、40分から50分くらいで全部解けるくらい、時間も余ったそうです。
ぜひ永井くんのように、間違えたところはしっかりと言語化して判断枠組を構築し、一枚の紙の中にまとめて反復していきましょう。
そうすることで、あなたの中にストックがどんどん増えていきます。
1-3.何年分の過去問を解けば良いか
先ほどもお伝えしましたが、共通テスト数学は誘導に乗れるかどうかがとても重要な教科です。
問題文が誘導になっていて、その誘導に気づいたら、その誘導の式を使う、その誘導で出てきた答えを使う、その誘導の考え方を使う…という風に解いたら、5秒で解き終わることもあります。
これを、自力で解こうとして解けなかったり、やたら時間がかかってしまい、タイムアップしてしまっているケースが結構多いです。
問題文がどういう誘導になっているのかを研究することが、過去問の研究の目的でもあります。
ですので、過去問をしっかりと研究していなかったら、高得点を取れるようにはなりません。
過去問を研究するために、最低でも5年分の過去問はチェックするようにしましょう。
そして、できれば10年分、さらに言うと15~20年分の問題を全て解いたら、かなりの共通点が見えてくると思います。
各年の問題を解く中で、どこに着目すべきだったのかを常に自分の中でフィードバックし、自分自身の手応えとして感じられるような復習をすることが大切です。
では、実際の具体例で見てみましょう。
センター数学2013年の2Bの大問3です。
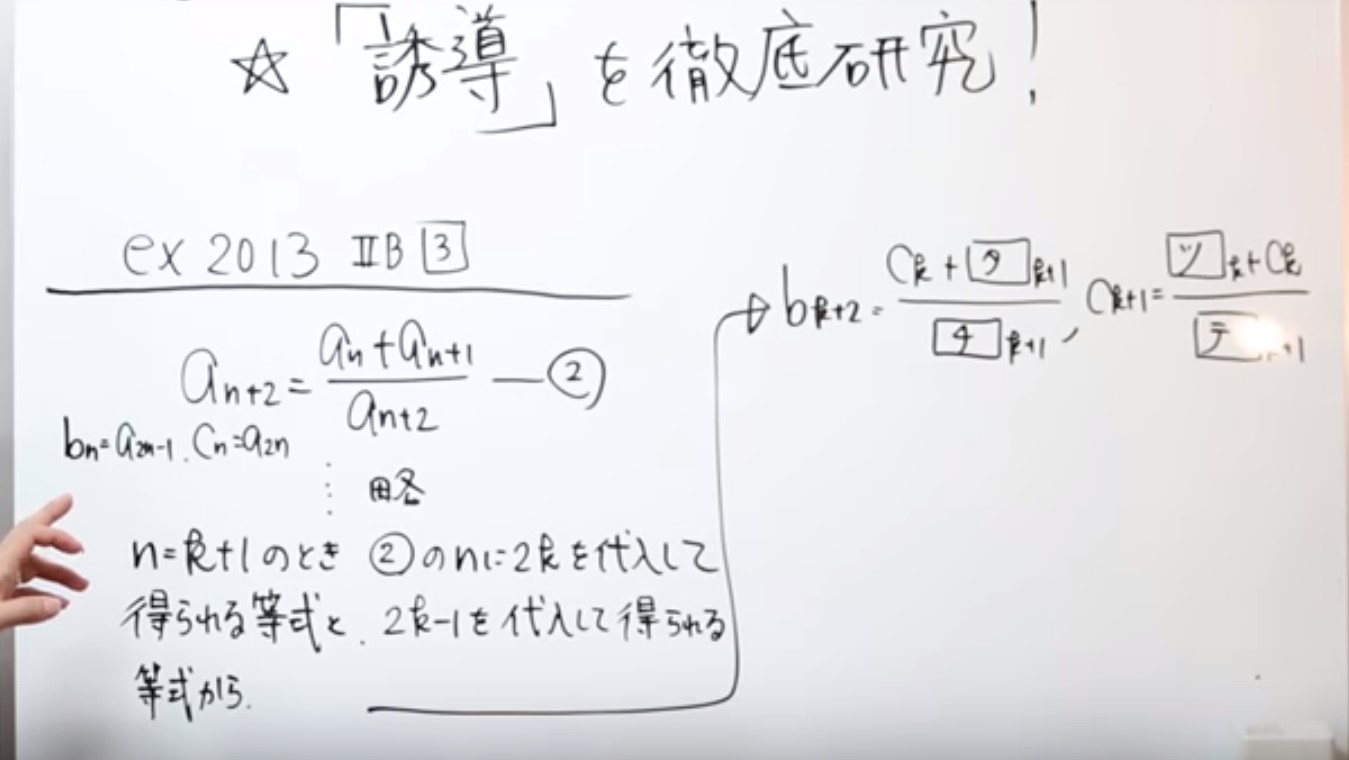
問題を全部は書けないですし、長々とは解説できないので、端的なポイントだけ説明します。
問題文には色々と書いてありますが、
an+2=an+an+1/an+2
という②式が与えられています。
bn=a2n-1
cn=a2n
といったようにに、普段ではあまり見ない形の問題になっています。
センターで誘導に従って解いていくように見えますね。
そして設問のスタートは、n=k+1の時、②のnに2kを代入して得られる等式と、2k−1を代入して得られる等式から、bk+2、ck+1を求めましょう、という問題になっています。
注目すべきは、この「から」っていう言葉です。
これは確実に前の文章を誘導として、この考え方を使い、ここで指示に従って解くようにと、因果関係の「〜〜だから、○○」ということを言っているのです。
「よって」とか「従って」という言葉を含めて、こういったワードは見落とさずに見つけるようにしましょう。
問題を見て何をしていいか分からない、止まってしまうという人は、こういうワードを見ていないのです。
研究の段階では、しっかりと意識しましょう。
例えば、②式のnに2kを代入するということで、代入してみたら、
a2k+2=a2k+a2k+1/a2k+2
という風に、nに2kを代入して得られる等式があります。
で、今度はnに2k−1を代入する。
これは、もう一方の式になる予想が立つので、スタートはまず2kを代入してみることです。
そして代入し、この求めた式と、形が似ているが、bとかaとか少し違うということで、②式のすぐ後にある、
bn=a2n-1
cn=a2n
この設定を見たときに、ゴールはbkとかにしないといけないので、
bn=a2n-1
を使えばできるのではないか、となります。
ということで、先の式を2でくくり、
a2(k+1)=a2k+a2k+1/a2k+2
として、
cn=a2n
なので、他の要素もどうなるのかを見ていけばよいのです。
2でくくったら2(k+1)となり、半分にしたものなので、ck+1が入ります。
同じように対応関係を見たらbが入る、となるわけです。
このようにして、問題文の誘導に従ったら、解けるようにできているのです。
そのヒントになるのは、「から」。
この誘導に従って、誘導を徹底研究していくことが、すごく大切です。
ここでは誘導の重要性について伝えたかったので、さらっと流れるようにお伝えしましたが、これを日々、最低5年分、できれば10年分、そして予想問題集なども解いていくことをおすすめします。
特に共通テストが命な人にとっては、こういった研究を早い段階から行なうようにしましょう。
1-4.共通テスト数学の過去問はいつから始めれば良いか
共通テスト数学の過去問は、おおよそ9月頃から始めるのがよいと思います。
先ほどお伝えした問題文の誘導を蛍光ペンなどでチェックしていきながら、思考の流れを矢印などで追うようにしましょう。
「この言葉があるから、この式に代入しなければいけない」と、目で追えるように、誘導を手書きで書き込んだノートを作るのもいいと思います。
過去問に直接書き込んでも構いませんので、何回も反復して自分の言葉にしていく練習をしてみてください。

2.共通テスト数学で計算時間を短縮して高得点を取る人の時間配分
共通テストの数学では、時間が足りないと言う人が多いです。
その理由の一つとして、計算でもたついてしまうことが挙げられます。
一つ一つ問題を見るたびに、手が動くまでに時間がかかってしまうのです。
では、どうすればいいのか。
まず、数学の問題を解く時に、「解法」と「計算」の2つに分けて考えて対策するようにしましょう。
ここでいう「解法」とは、書籍『大逆転勉強法』でお伝えしているセルフレクチャーのことです。
一つ問題を見て、その解き方を口で答えていく。
ただし、計算はおこなわない。
セルフレクチャーをすることで、解法がすぐにスラスラと出てきて、考え込む時間がなくなるような状態を目指します。
そして、「計算」に関しては、九九はもちろんのこと、
例えば11×11、12×12、13×13など、よく出てくるような掛け算や計算式は、頭の中に入れておくようにします。
理想を言えば、九九のように体が反射するような状態にもっていきます。
実際の計算では、頭を使うのではなく、手が勝手に動く状態になるまで、計算力を高めておく必要があります。
そうすると、問題を見た時に「この問題はどういう風に解いたら良いのか?」がパッと思い浮かび、解法がわかった瞬間に手が勝手に計算を始めている。
計算をしている時に頭を休めたり、もしくは頭の中で先読みをしていって、計算している時に次の展開を考えている状態にできれば、ベストです。
そうすることで、「(1)の計算が終わった。では(2)はどうしよう。(2)が終わった。では次の(3)はどうしよう」という風に立ち止まるのではなく、
「(1)を解いている時には(2)を考えていて、(2)を解いている時には(3)を考えている」というくらい、頭と手が別々に作業しているくらい、計算というのは脳に負荷をかけません。
逆に言うと、脳には「この問題を解くにはどうすればいいのか」と、解法を考えることに専念させてあげることが大切なのです。
脳のエネルギーはある程度限られていますので、計算にエネルギーをかけてしまうと、当然解法を考えるのにエネルギーをかけられなくなってしまいます。
ですので、徹底的に問題集を反復練習して、簡単な計算は体が勝手に反応するくらいの状態にするようにしましょう。
こうすることで、脳は計算ではなく解法の方にエネルギーをかけることができるので、結果として時間が短縮されて、高得点を取ることができます。
解法の部分と計算の部分を同時並行に行ない、ぜひ自分のバイブル本を何度も何度も反復練習して徹底的に仕上げて、共通テスト数学を攻略していきましょう。
3.共通テスト数学でミスを防ぐための注意点
共通テストはとにかく時間との戦いです。
迷いながら解いていると、当然遅くなってしまう。
考えている時間が長いと、スラスラと流れるように解けないわけです。
では、この迷いはどこから生まれるのか。
それは、普段から徹底的にシミュレーションできていないからです。
丁寧に考えた上で「絶対これはこうなんだ」という風に、確信を持って解法を選べていないからです。
これを具体的な例で紹介したいと思います。
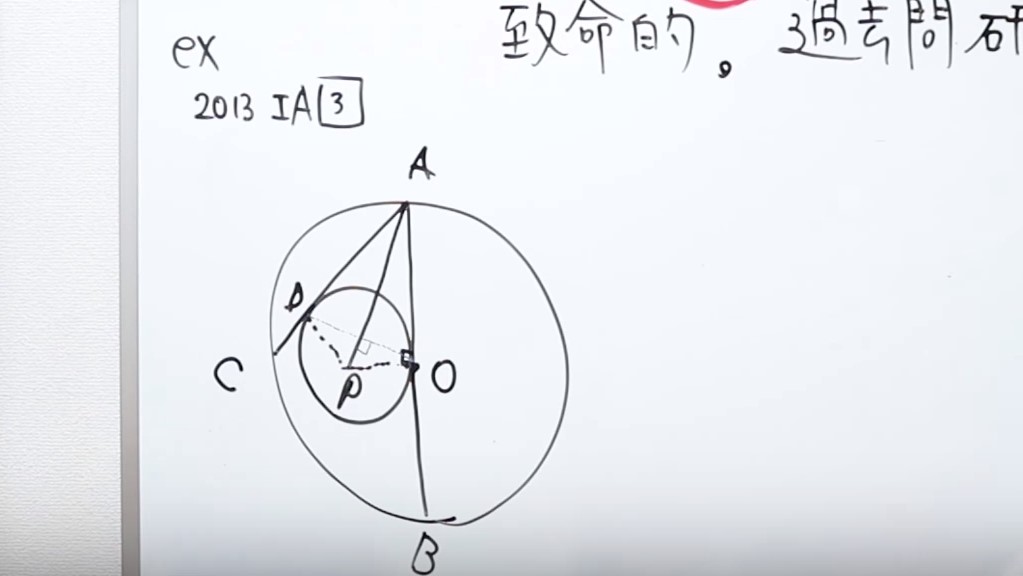
これはセンター数学2013年の1Aの大問3ですが、ある時、受験生にこう聞かれました。
「ODの長さ求める問題なんですが、なぜここが90度になるんですか」
解いている時「これは本当に90度なのか」と迷ってしまうと、ODの長さを求めるのが少し遅くなってしまいます。
結論から言うと、この角度は90度ですが、これに対する迷いは無くしておかないといけません。
それは普段の勉強の時に、一般的な問題を考えた時、たとえば円があって、その円に対して接線を引いた時、それぞれ90度になりますよね。
共通の線を引いて、長さが同じ、合同な三角形です。
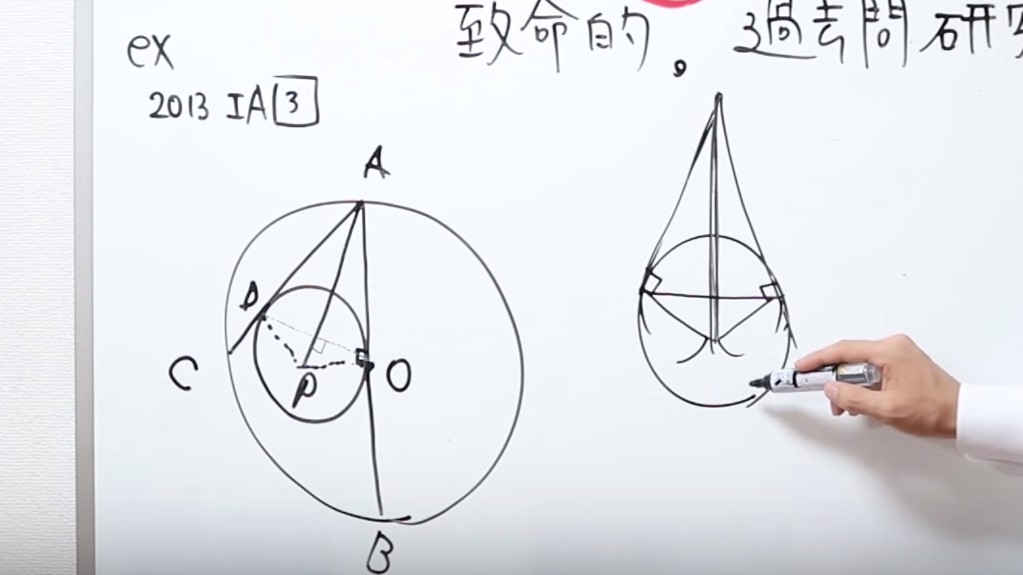
合同三角形ですが、ここに線を引いたら、これも長さが同じ二等辺三角形になります。
二等辺三角形で、底角も等しいので、ここの長さもここの長さも同じです。
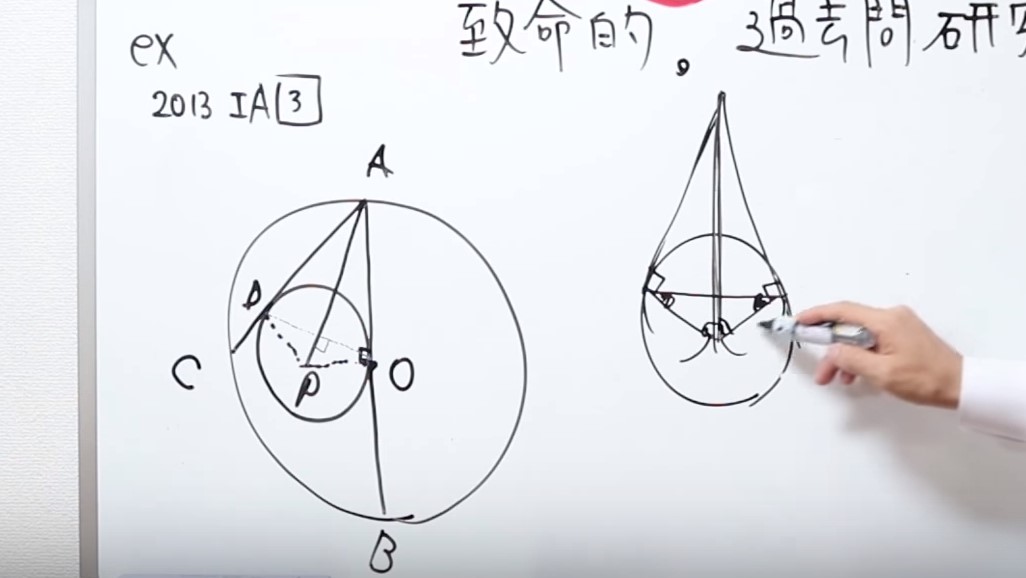
しかも、ここの黒い角度が同じですよね。これが合同なので、ここも合同になる。
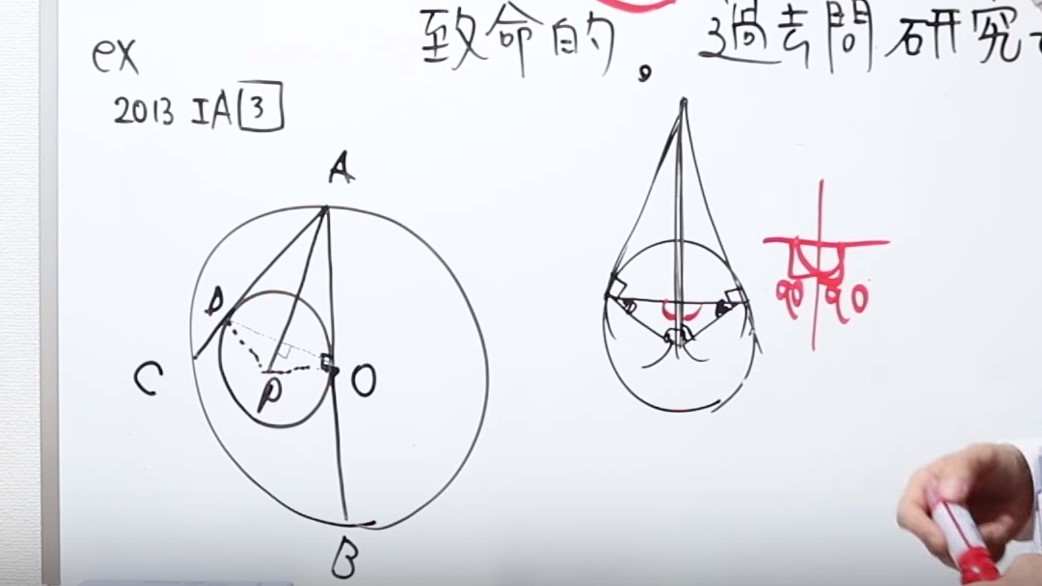
ここの赤い角度は、おのずと同じになります。
というのも、180度が同じ角度になるのは、90度としか言えないので、赤い角度はそれぞれ90度になります。
そして、真ん中の直線は、弦にそのまままっすぐに降ろしているので、垂直二等分線と言えます。
二等辺三角形で、弦に垂直に引いた垂直二等分ですが、これも本番で迷わないためには、徹底的に普段の勉強で煮詰めていかないといけません。
そのためにも、過去問をやるべきなのです。
過去問で迷うことがあったら、迷ったところが「本当に90度なのか」を説明して、90度という確信を持てるように復習すべきです。
しっかりと時間を取って復習をするようにしましょう。
実際に、過去問を解きっぱなしの人が多いです。
問題を間違えていなかったとしても、自分が迷ったところで立ち止まらず、考えないのです。
そうすると、次に同じ問題を解いた時に確信を持てないので、迷いになったり、不安になったりするのです。
不安になりながら解くと、IQが下がり、思考力が低下します。
不安にならないためにも、過去問解いた時に自分が詰まったところは、一度立ち止まって徹底的に考えるようにしてください。
そして、なぜそうなるのか、原理・原則をしっかり理解してから、次に進んでほしいと思います。
4.思考実験でセンターの点数を上げる!
そして、センター数学の点数をさらに伸ばすコツとして、「思考実験」があります。
「思考実験」とは、試験本番までに自分の頭の中でも手書きでもいいので、出会った問題に対してなぜこういう風に解くべきなのか、何回も実験を重ねていく、ということです。
思考実験をして、この可能性はどうなのか、この解法はどうなのか、と確かめていかないと、確信を持って解答が選べなくなってしまうので、自分で思考実験をしていくことが非常に重要です。
思考実験のやり方について、具体的な例で説明しましょう。
例えば、
「xが実数であるときx2+xが有理数ならば、xは有理数である。」
これの真偽を調べる問題が出てきた時、その真偽を調べるために反例を考えて、
例えば、x=√2−1/2を反例と考えたときに、
x2+xはxでくくれるので、x(x+1)という風に考え、
代入したら、
=(√2−1/2)(√2+1/2)
となるので、
=2−1/4
=7/4
になるということで、
「xが実数であるときx2+xが有理数ならば、xは有理数である。」
と言えるかどうか、ということなのです。
xは無理数でも有理数になり得るので今回は偽である、と言えるのですが、この反例を挙げたときに、
√2−2/1
の何が都合がよかったのか、なぜこれが良いのか、なぜこの反例を挙げるのか、といったことは、色々試してみないとわからないケースがあります。
√2ではなぜダメなのか、なぜ分数にしているのか、ということです。
実際に、√2で試しても反例になっていなかったりと、自分で試さないと実感が湧かないことが多いのです。
模範解答をパッと見たら、この解法はこういうものだという理解になりますが、解法を理解していくのと同時に、「この場合はどうなのか?」という風に、本番までにありとあらゆる可能性を試しておくのです。
本番で試していると遅いので、本番までに5年分を徹底研究するといいでしょう。
なぜ10年分や15年分ではないかというと、5年分ぐらいでないと、時間的に徹底研究ができないからです。
徹底研究と問題を解きまくるのは、少し違います。
過去問を徹底研究するためには、まず問題の解きまくりで、いろいろなシチュエーションや場面で解いていく。
そして、間違えたところだけ模範解答をしっかり読み、「こうすればよかったのか」と復習する。
しかし、5年分に関しては、掘り下げて、どんな可能性があるのか、何故この可能性がなかったらダメだったのか、というところは、しっかりと煮詰めて考えていくのです。
自分の頭で考えうる範囲で、この可能性は、この場合は、この状況だったら、数字が変わったらどうなるか、というのを徹底研究してほしいと思います。
模範解答をただ鵜呑みにするだけでなく、模範解答に書いていることに一回ツッコミを入れていく。
そうすることで、その過去問に書いている模範解答の必然性や、なぜこう解くべきなのかがしっくりくると思います。
5年分の徹底研究をおこない、問題の解きまくりに移れば、共通テスト数学は確実に点数が上がっていくでしょう。
ぜひ問題を徹底研究してみてください。













